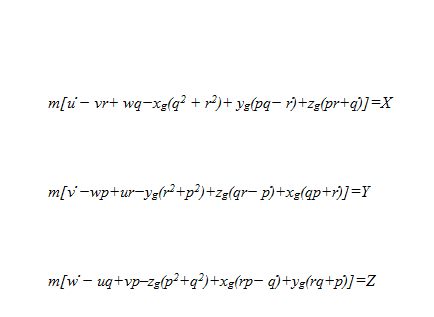
Figure 2.1: Body-fixed and earth-fixed reference frames.

The motion of the body-fixed frame is described relative to an inertial reference frame. For marine vehicles it is usually assumed that the accelerations of a point on the surface of the earth can be neglected.

An earth-fixed reference frame XYZ can be considered to be inertial. This suggests that the position and orientation of the vehicle should be described relative to the inertial reference frame while the linear and angular velocities of the vehicle should be expressed in the body-fixed coordinate system. The general motion of a marine vehicle in 6 DOF can be described by the following vectors:

; ;

; ;

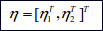
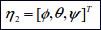
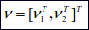
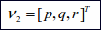
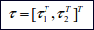
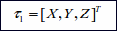
; ; _(2.1)

Here η denotes the position and orientation vector with coordinates in the earth-fixed frame, νdenotes the linear and angular velocity vector with coordinates in the body-fixed frame and τ is used to describe the forces and moments acting on the vehicle in the body-fixedframe. Now the kinematic equations relating the body-fixed reference frame to the earth-fixed reference frame will be derived.

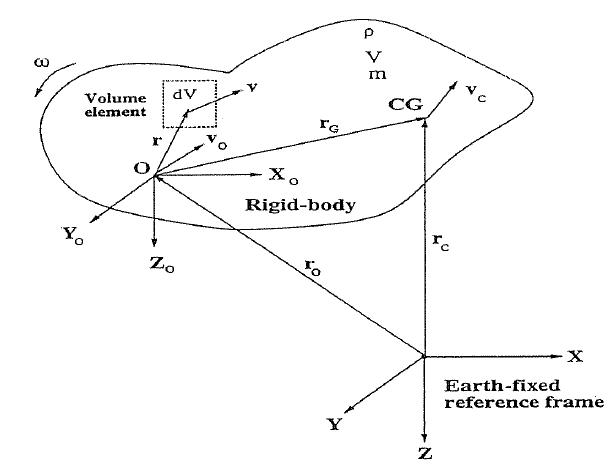
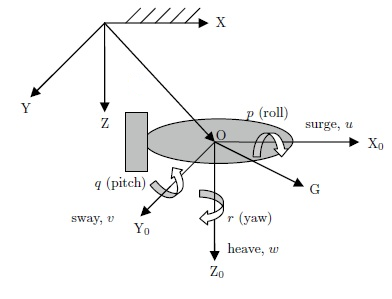
Figure 2.2: The inertial, earth-fixed non-rotating reference frame XYZ and the body fixed rotating reference frame X₀Y₀Z₀.

For marine vehicles it is desirable to derive the equations of motion for an arbitrary origin in a local body fixed coordinate system to take advantage of the vehicle's geometrical properties.Since the hydrodynamic and kinematic forces and moments are given in the body fixed reference frame we will formulate Newton's laws in the body-fixed reference frame.

When deriving the equations of motion it will be assumed that:

(1)the vehicle is rigid and

(2)the earth-fixed reference frame is inertial .

To derive the equations of motion for an arbitrary origin in a local body-fixed rotating coordinate system we need the formula: